Introduction
A Social Network is a collection of social actors (peoples, organizations, co-workers etc.) and the connections or relations between those actors. Social networks are best represented by Graphs where vertices (nodes) represent the social actors and edges (links) represent the relation between those actors.
Two peoples can have multiple relations, for example, they can be friends as well as co-workers, resulting into multiple (parallel) edges between the vertices representing them in a social network graph. Sometimes multiple or parallel edges are handles by assigning each of them a suitable weight, for example, edge representing “friends” can be weighted higher than the edge representing “following” relation.
The relationships between people keep evolving with time, new connections appear and sometime old ones disappear and hence the edges in a social network keep changing with time. For these reasons, social networks are very dynamic by nature and they grow very fast which makes it a challenging task to analyze and predict their future behavior.
Real world examples of social network include the set of friends, families and followers with edges defining relations between them; or the set of authors, or scientists with edges defining their relations (co-authors, research partners etc.) with others in the network.
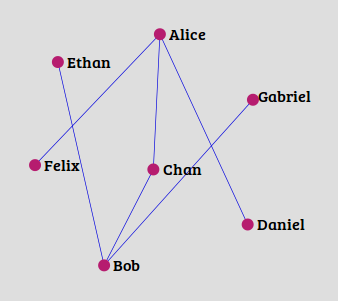
The Problem
So, given a social network, can we predict how the future network would look like? Or what new edges are likely to be formed in the future? In other words, to predict the likelihood of formation of new edges between any two nodes currently not connected with any edge.
This problem is known as the link prediction problem in the social networks and it is a part of social network mining or analysis. The link prediction problem can also be extended to inferring missing (erased or broken) links in the network, for example, in a meeting of three persons, the (missing) name of third participant can be predicted if the other two persons and their past meetings in the network are known.
Real world examples of link prediction are suggesting friends and followers on social networking websites, suggesting relevant products to customers in e-commerce, providing suggestions to scientists or researchers to work together based on their fields of interests, and suggesting organizations to work with other organizations in their network.
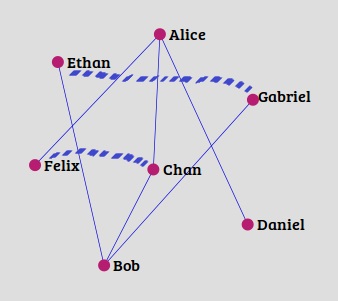
Methods
Various methods have been developed to solve link prediction problem based on node neighbors and paths length between nodes. Though, no method can be said to be perfect, the following methods do really perform much better than a random predictors:
Common Neighbors: This method calculates a score based on the number of common neighbours (mutual friends, followers, interests or other features) of nodes x and y. Higher the number of common nodes, higher are the chances that they will have an edge (relation or collaboration) in the future.
Score(x, y)=Nx ∩ Ny
where, Nx = neighbours of x and Ny = neighbours of y
Jaccard Coefficient: Jaccard Coefficient calculates the probability that nodes x and y have a common feature, for a randomly selected feature f out of set of all neighbors around x and y.
This method might look similar to the Common Neighbors method but its predictions are not exactly same as of the latter.
JC(x, y) = (Nx ∩ Ny) / (Nx ∪ Ny)
where, Nx = neighbors of x and Ny = neighbors of y
So, the higher the fraction of neighbors of x and y is common, the higher the probability of a link between nodes x and y.
Adamic – Adar (Frequency weighted common neighbors): Adamic and Adar proposed this formula which weighs the common neighbors with smaller degree more heavily. This means if x and y share one or more common neighbors which are not much popular in the network, the chances of x having an edge with y in future are higher.
AA(x, y) = ∑(z ∈ (Nx ∩ Ny)) 1/ log Nz
where, Nx = neighbours of x
Ny = neighbours of y
Z = common neighbors of x and y
Nz = neighbors of z
To understand this formula, one can simply think of two persons x and y living in the same city (common feature f) and other two persons x’ and y’ studying same subject in same university (common feature f’); we know that cities are more popular than subjects in a university i.e. number of nodes connected to the city are higher than the node connected to a subject; hence the chances of having x’ and y’ an edge in future would be higher (they share less popular neighbor(s)).
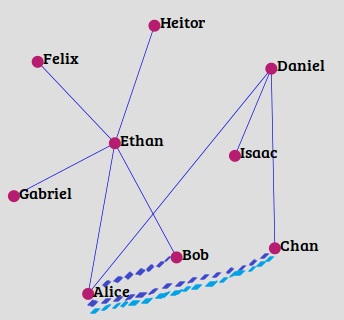
Preferential Attachment: This method states that the probability that a new future edge involves node x is directly proportional to neighbors of x. In real world, it matches the idea – rich become richer. In other words, more the number of current friends, higher are the chances of making new friends in future. Hence, the preferential attachments score of two nodes x and y is calculated as:
Score(x, y) = Nx × Ny
where, Nx = neighbours of x and Ny = neighbours of y
Applications
Friendship and Dating: It is the most popular use case of link prediction. Almost all the friendship and dating websites use it to suggest friends/families or dating partners to their users.
These suggestions are often based on nodes representing users, locations, age, education, work history, likes or the nodes they like or follow. These same is also used in matrimony websites to suggest their users the best matching partners.
E-commerce: E-commerce websites such as online shopping use the link prediction methods to suggest various products to their users. These sites maintain the data of their users including their purchase history which is used to analyze the user’s behaviors and provide the most probable suggestions.
For example: In a particular age group of users, there might be a trend to buy certain fashionable clothes, hence the recommendation engine can be instructed to weigh more to recent behaviors to predict the right product to the right customer or right time.
Work Organizations: By analyzing the employee data, organizations can build systems to suggest their employees best matched project or team to work with. Once employees are assigned to a team having common interests, they not only can do the best, but also build healthy work environment.
Large organizations can also utilize link prediction methods in successfully maintaining positive relations with old clients and collaborating with new clients to grow their client network.
Public Security: It is very hard to predict the crimes to be committed in the future and individuals behind those but by analyzing the criminals and terrorists network, the links which have not been seen so far, can be predicted which might be helpful in predicting the nature, place and the involved individuals.
Research and collaborations: Research in a field is often a long and tedious process which can be made interesting and more successful by bringing together the scientists with more common interests and goals. Large network of scientists around the world and their published papers, ongoing projects and university relations can be utilized to bring best scientists together to solve the problems.
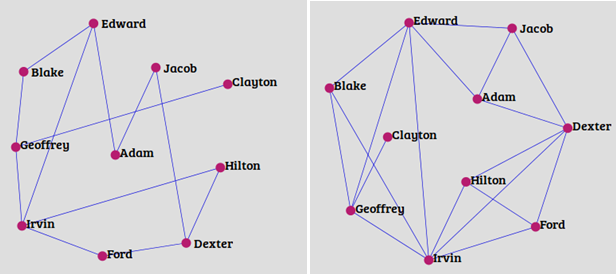
An Example
Given the below snapshot a social network, we will use Adamic Adar method to calculate the prediction scores for each of the 10 nodes in the picture.
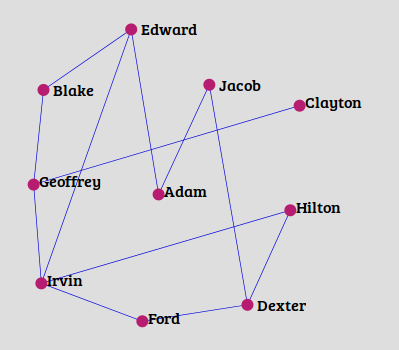
As discussed above, Adamic Adar method ranks higher to the new connection (currently not existing) between nodes who share less popular nodes in the network.
Using the below formula:
AA(x,y)=∑(z∈(Nx∩Ny)) 1 / logNz
For Adam and Dexter:
Z: common neighbours of Adam and Dexter: {Jacob}
Nz = N(Jacob) = 2
AA(Adam,Dexter)= 1/log(2) = 1/0.6931= 1.4427
When we apply the same formula for all nodes in the network, we get the scores as shown in the below table:
| Adam | Blake | Clayton |
|---|---|---|
| Dexter, 1.4426950408889634 | Irvin, 1.8204784532536746 | Irvin, 0.9102392266268373* |
| Irvin, 0.9102392266268373 | Adam, 0.9102392266268373 | Blake, 0.9102392266268373* |
| Blake, 0.9102392266268373 | Clayton, 0.9102392266268373 | *(same score for both) |
| Dexter | Edward | Ford |
|---|---|---|
| Irvin, 2.8853900817779268 | Geoffrey, 2.164042561333445 | Hilton, 1.631586747071319 |
| Adam, 1.4426950408889634 | Jacob, 1.4426950408889634 | Jacob, 0.9102392266268373 |
| Hilton, 0.7213475204444817 | Edward, 0.7213475204444817 | |
| Ford, 0.7213475204444817 | Geoffrey, 0.7213475204444817 |
| Geoffrey | Hilton | Irvin |
|---|---|---|
| Edward, 2.164042561333445 | Ford, 1.631586747071319 | Dexter, 2.8853900817779268 |
| Hilton, 0.7213475204444817 | Jacob, 0.9102392266268373 | Blake, 1.8204784532536746 |
| Ford, 0.7213475204444817 | Edward, 0.7213475204444817 | Adam, 0.9102392266268373 |
| Geoffrey, 0.7213475204444817 | Clayton, 0.9102392266268373 |
| Jacob |
|---|
| Edward, 1.4426950408889634 |
| Hilton, 0.9102392266268373 |
| Ford, 0.9102392266268373 |
In the above table, higher the score value, the chances are higher that the nodes would connect in future. For example, chances of Blake connecting with Irvin are more than that with Adam.
The full working code for the link prediction problem can be found at BitBucket and the notebook at DataBricks which is written in python and uses Apache Spark as the computing framework.
Below is the image which shows how the network would look if we connect each node (ignoring the Clayton as its predictions scored lower than others) with their first top predicted node:
Future Scope
Although many efforts have been put in developing link prediction algorithms in the past, but still there is much room for the improvement.
The predictions can be made more accurate by refining the edges, for example – assigning large weight to recent edges and small to old ones and by introducing psychology to better handle the human characteristics present in the network.
Sometimes, in the network, there may be presence of duplicate, inactive, fake, or robotic nodes which can be better handled by first identifying and weighing them differently from active, real and human nodes. For examples, we often see duplicate nodes representing save cities, universities or public figures (artists) on social networking sites which, if not handled properly, would show false positive behavior and incorrect score of predictions.
Social network are very large and processing them takes too much time which further increase as the network grows, hence faster algorithms can be developed. In addition, supervised algorithms based on classifications and regressions can be developed which might result in better predictions.
Conclusion
We discussed that social networks are made of social actors and connections or relations between them and these networks are best represented by Graphs where nodes are social actors and edges are the connections between nodes. Social networks are often very large and grow at a fast rate.
These social network graphs consist of so much data that it is a challenging task to process and do the analysis. In the link prediction methods, we take a small snapshot of these large networks to analyze and predict future edges between the nodes.
As discussed, there are many potential areas of our social life where link prediction plays many important roles and still there are a lot of fields where it has open opportunities.
We have also seen various methods to solve the link prediction problems but none of them can be said to be the best as they all introduce incorrect predictions too. But they can be further improved by incorporating some additional methods such as refining the dataset or introducing psychological studies. Also, many machine learning methods have been evolved in recent years which provide more ways to improve these predictions.
References
Liben-NoWell , David and Kleinberg, Jon, 2004, The Link Prediction Problem for Social Networks









